Perbandingan Trigonometri Sinus Kosinus dan Sudut Istimewa Perbandingan Trigonometri

Tujuan Pembelajaran :

Peserta didik dapat menentukan nilai perbandingan trigonometri sinus dan cosinus suatu segitiga siku-siku dengan sudut istimewa trigonometri.

Perhatikan Gambar Dibawah Ini!

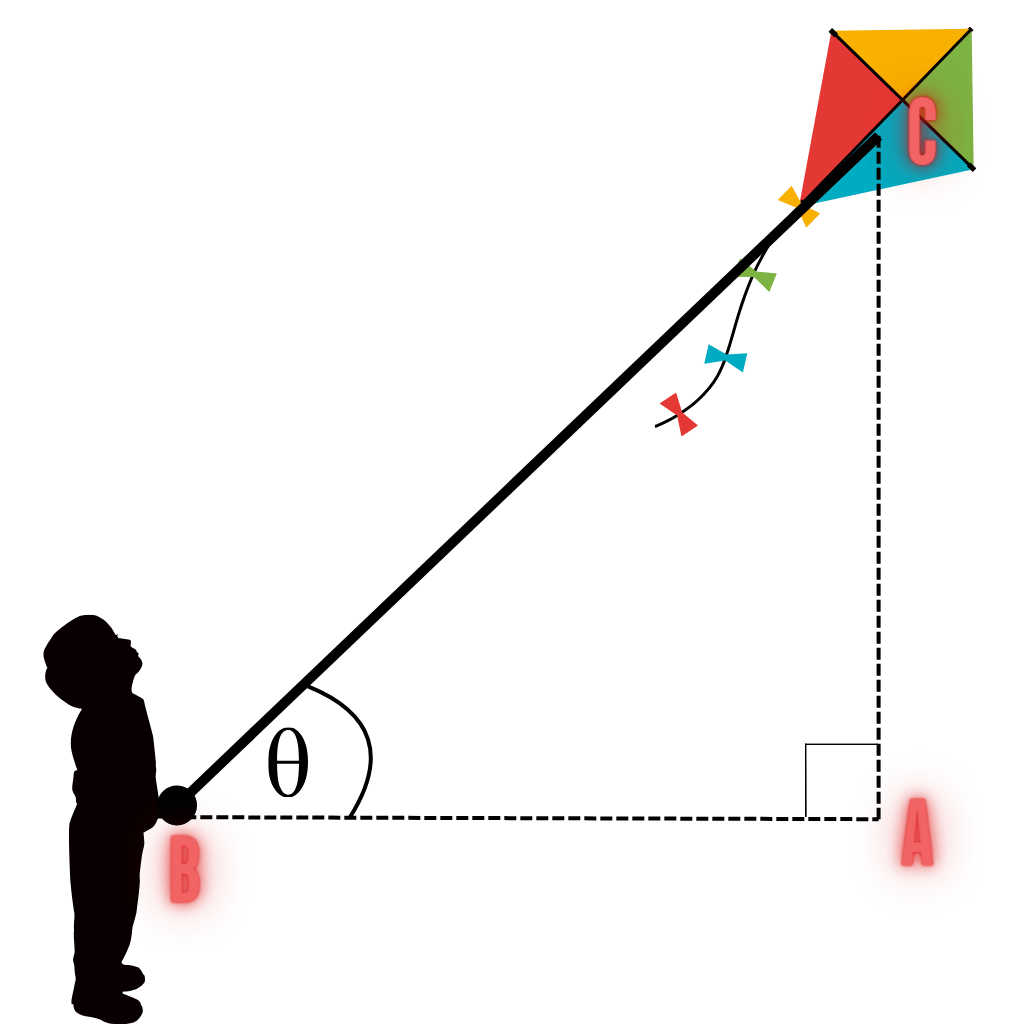
Pada gambar diatas terdapat seorang anak yang sedang bermain layang-layang dan membentuk segitiga siku-siku saat diberikan garis putus-putus, hal tersebut membentuk perbandingan trigonometri dengan rumus sinus dan kosinus, kita dapat mengetahui perbandingan trigonometrinya, dengan rumus sebagai berikut :

Perbandingan sinus ditulis dengan rumus: s i n θ = s i s i d e p a n s i s i m i r i n g = A C B C

Perbandingan kosinus ditulis dengan rumus: cos θ = s i s i s a m p i n g s i s i m i r i n g = A B B C

Lalu, pada perbandingan trigonometri terdapat sudut-sudut yang dinamakan sudut istimewa perbandingan trigonometri, sudut istimewa perbandingan trigonometri yaitu sudut yang nilainya dapat ditentukan secara eksak.
Contoh Soal:
Misalkan Anda akan membuat tumpeng. Cetakan tumpeng tersebut berbentuk kerucut dengan sudut kemiringan θ= 60° dan panjang garis pelukisnya adalah 50 cm. Berat nasi tentu bergantung apda volume tumpeng (volume kerucut). Tentukan volume tumpeng (volume kerucut)!

Jawaban:
Tumpeng dimodelkan sebagai kerucut. Tumpeng yang akan Anda hitung volumenya dimodelkan seperti gambar dibawah ini.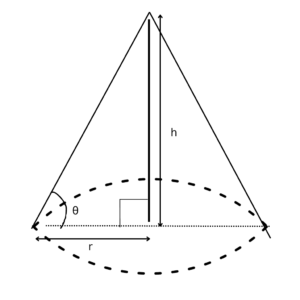
Maka jari-jari r bisa ditentukan dengan perbandingan cosinus.
cos θ= s i s i s a m p i n g h i p o t e n u s a = r s ↔ r = s cos θ
                                                      = (50) cos 60°
                                             =(50)(0,5)
                                        =25 cm

Karena diameter adalah dua kali jari-jari, maka diameternya adalah 2 × 30 cm = 60 cm.
Tinggi kerucut h bisa ditentukan dengan perbandingan sinus.
sin θ = s i s i d e p a n h i p o t e n u s a = h s ↔ h = s sin θ
                    = (50) sin 60°
                                                  = (50) (0,8)
                                           = 40 cm

Maka, didapatkan hasil tinggi tumpeng adalah 40 cm.
Hitung volume kerucut.
V = π r 2 h 3 = 3 , 14 ( 25 ) 2 ( 40 ) 3 cm 3 =26.166,67 cm 3 = 26,16 dm 3 = 26,16 L.
Dengan demikian, volume tumpeng adalah 26,16 liter.